发布算法题解11 分钟读完 (大约1663个字)  次访问

2021复旦机试回顾

2021年复旦大学计算机专业预推免机试题，一共3道题，都比较常规，主要考察动态规划。

第一题

将 n 个正整数存放于一个一维数组中，编写一个程序，将数组中所有的奇数存放于所有的偶数之前，要求尽可能少用临时存储单元并使时间复杂度达到 O(n)。输入：一维数组；输出：符合要求的一维数组。

解题思路

使用类似快排的思想，定义前后2个指针，前指针向后移动直到指向一个偶数；后指针向前移动直到指向一个奇数，然后交换这2个数的位置。然后继续移动2个指针直到相遇。由于2个指针一共只需遍历一遍数组，所以时间复杂度是O(n)，同时数字是原地交换的没有使用额外空间。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
/**
 * 将 n 个正整数存放于一个一维数组中，编写一个程序，将数组中所有的奇数存放于所有的偶数之前，
 * 要求尽可能少用临时存储单元并使时间复杂度达到 O(n)。
 * 输入：一维数组；输出：符合要求的一维数组。
 **/
#include <bits/stdc++.h>
using namespace std;

bool is_odd(int x)
{
    return x % 2 == 1;
}

int main()
{
    int a;
    vector<int> nums;
    while (cin >> a)
    {
        nums.push_back(a);
    }

    int n = nums.size();

    int l = 0;
    int r = n - 1;

    while (l < r)
    {
        while (l < r && is_odd(nums[l]))    // 从左到右遍历，直到一个偶数
        {
            l++;
        }
        while (l < r && !is_odd(nums[r]))   // 从右到左遍历，直到一个奇数
        {
            r--;
        }
        if (l < r){
            swap(nums[l++], nums[r++]);     // 原地交换两数
        }
            
    }

    for(auto& i:nums){
        cout<<i<<" ";
    }
}

测试用例

  1. 1
    2
    3
    4
    # in
    1 2 3 4 5 6 7
    # out
    1 7 3 5 4 6 2 
  2. 1
    2
    3
    4
    # in
    2 4 6
    # out
    2 4 6
  3. 1
    2
    3
    4
    # in
    4 6 8 1 5
    # out
    5 1 8 6 4 
  4. 1
    2
    3
    4
    # in
    <空>
    # out
    <空>

第二题

给定 n 个小区之间的交通图， 并用二维数组 A[n][n]表示，即若小区 i 与小区 j 之间有路，则 A[i][j]表示这条路的长度。现计划在这 n 个小区中选定一个小区建一所医院，使距离医院最远的小区到医院的路程尽可能缩短。编写一个程序解决上述问题。
输入：二维数组；输出：建医院的小区。

解题思路

本题要先以每个点为起点，找到到达其他点的最短路径，算出到达最远点的距离。然后选出最远点距离最短的那个点。所以本题是一个多源最短路径问题，我采用了Floyd 算法，用的是动态规划的思想，如果顶点i和j之间存在一条经过k点的路径，能得到一条更短的路径，则可以将 k 作为其最短路径的中间点，更新最短路径长度。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
/**
 * 给定 n 个小区之间的交通图， 并用二维数组 A[n][n]表示，即若小区 i 与小区 j 之间有路，
 * 则 A[i][j]表示这条路的长度。现计划在这 n 个小区中选定一个小区建一所医院，使距离医院
 * 最远的小区到医院的路程尽可能缩短。编写一个程序解决上述问题。
 * 输入：二维数组；输出：建医院的小区。 
 **/
#include <bits/stdc++.h>
using namespace std;


int main()
{
    int n; // n 个城市
    cin >> n;
    // 每2个城市间的最短路径。初始：直达路长度 或 无穷远
    vector<vector<int>> dist(n, vector<int>(n, INT_MAX));

    // 输入
    int tmp;
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            cin >> tmp;
            if (i == j) // 到自身的距离为0
            {
                dist[i][j] = 0;
                continue;
            }
            
            if (tmp > 0)
                dist[i][j] = tmp;
        }
    }

    // 用 Floyd 算法，求每2个点之间的最短路
    for (int k = 0; k < n; k++) // 中间点k
    {
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < n; j++)
            {
                // 需要保证k到两点均存在通路
                if (dist[i][k] < INT_MAX && dist[k][j] < INT_MAX && (dist[i][k] + dist[k][j] < dist[i][j]))
                    dist[i][j] = dist[i][k] + dist[k][j];
            }
        }
    }


    int min_dis = INT_MAX;  // 路径的最小值
    int city=0;     // 所选城市编号
    for(int i=0;i<n;i++){   // 假设以每个城市作为中心点，计算其他城市到 i 点最远的距离
        int max_dis_to_i=0;     // 到 i 点最远的距离
        for(int j=0;j<n;j++){
            if(i==j)continue;
            max_dis_to_i=max(max_dis_to_i,dist[i][j]);
        }
        if(max_dis_to_i<min_dis){
            min_dis=max_dis_to_i;
            city=i;
        }
    }

    cout<<city;
}

测试用例

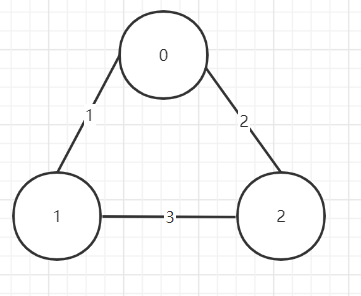
  1. 1
    2
    3
    4
    5
    6
    7
    # in
    3
    0 1 2
    1 0 3
    2 3 0
    # out
    0

    image-20210923110756745

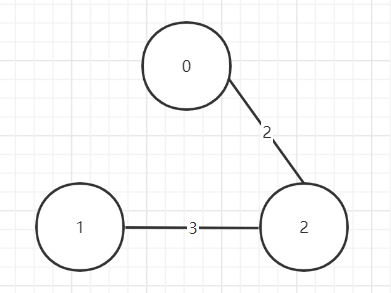
  2. 1
    2
    3
    4
    5
    6
    7
    # in (0,1间没路)
    3
    0 0 2
    0 0 3
    2 3 0
    # out
    2

    image-20210923110815131

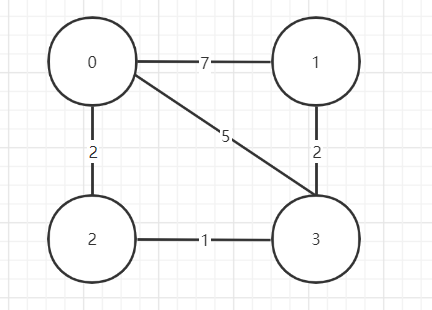
  3. 1
    2
    3
    4
    5
    6
    7
    8
    # in
    4
    0 7 2 5
    7 0 0 2
    2 0 0 1
    5 2 1 0
    # out
    2

    image-20210923110909811

第三题

给定一个长为 n 的序列， 其中序列中的元素都是 0～9 之间的整数。 现在要从序列的第一个位置走到最后一个位置，每次要么往后走一步，要么走到下一个与当前位置元素相同的位置， 编写一个程序求所需要的最少步数， 要求时间复杂度 O(n)。
输入： 整数序列；输出： 最少步数。

解题思路

本题我采用了动态规划的思路，假设$dp[i]$表示从位置0走到位置i的最少步数，$last[i]$表示i位置的数上一次出现的位置，由于每一步有2种选择，那么可以写出递推式$dp[i]=\min(dp[i-1]+1,dp[last[i]]+1)$。最终答案即为$dp[n-1]$.

所以问题就转化为求解$last[]$数组，由于本题规定只有0~9之间的数字，所以不妨定义一个长度为10的滚动数组$digit_last[]$记录每个数字上次出现的位置，这样只需遍历一遍原始数组，就能构造出$last[]$.

总体而言，构造$last[]$数组时间复杂度为O(n)，求解dp的复杂度同样是O(n)，所以总体复杂度为O(n).

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
/**
 * 给定一个长为 n 的序列， 其中序列中的元素都是 0～9 之间的整数。 现在要从序列的第一个位置走到最后一个位置，每次要么往后走一步，要么走到下一个与当前位置元素相同的位置， 编写一个程序求所需要的最少步数， 要求时间复杂度 O(n)。
 * 输入： 整数序列；输出： 最少步数。  
 **/
#include <bits/stdc++.h>
using namespace std;

int main()
{
    int a;
    vector<int> nums;
    while (cin >> a)
    {
        nums.push_back(a);
    }

    int n = nums.size();
    if (n == 0)
    {
        cout << 0;
        return 0;
    }
    vector<int> digit_last(10, -1); // 记录每个*数字*上一次出现的位置
    vector<int> last(n, -1);        // 记录与该*位置*数字相同的上一个位置

    // 构造last[]数组
    for (int i = 0; i < n; i++)
    {
        last[i] = digit_last[nums[i]];
        digit_last[nums[i]] = i;
    }

    vector<int> dp(n);
    dp[0] = 0;

    for (int i = 1; i < n; i++)
    {
        dp[i] = dp[i - 1] + 1;  // 往后走一步

        if (last[i] != -1)  // 如果可以跳跃到此处
        {
            dp[i] = min(dp[i], dp[last[i]] + 1);    // 2种走法的最小值
        }
    }

    cout << dp[n - 1];
}

测试用例

  1. 1
    2
    3
    4
    5
    6
    7
    # in
    0 1 0 3 4 1
    # out
    2

    # 解释：
    0->1->1
  2. 1
    2
    3
    4
    5
    6
    # in
    0 1 2 3 4 5
    # out
    5
    # 解释：
    0->1->2->3->4->5
  3. 1
    2
    3
    4
    5
    6
    # in
    9 8 9 5 9 2 5 1
    # out
    4
    # 解释：
    9->9->5->5->1
  4. 1
    2
    3
    4
    # in
    <空>
    # out
    0

2021复旦机试回顾

https://blog.luzy.top/posts/2309874471/

作者

江风引雨

发布于

2021-10-07

更新于

2024-07-10

许可协议

CC BY 4.0

#

喜欢这篇文章？打赏一下作者吧

评论

目录

×